Discovering Player Tracking in a Minimal Tic-Tac-Toe Transformer

Interpreting Machine Learned Models

Mechanistic interpretability has been gaining prominence as the technical approach to AI safety and alignment. Mapping the algorithms used by models would lead to tools for understanding, analyzing, and manipulating model decision making and risks. The results so far have been promising! Anthropic pushed their LLM, Claude, into constantly discussing the golden gate bridge through these mechanistic understandings and in another investigation decomposed the high level logic of how it performs arithmetic. At the most fundamental level others have found the precise mathematical processes utilized by small toy models in performing operations such as modular addition.

From the utilitarian perspective mechanistic insights could underpin data and metric driven regulation, training schedule and data quality characterization, and to the horror of staunch AI Safetyists, capability improvements. The scientific vision is also pretty tantalizing. AI models are “grown not designed”. It’s easy to further extend the parallel to biology - hold some state space under optimization pressure long enough and you get incredible, yet opaque, algorithms. Disentanglement of those emergent algorithms requires new tools, new theories, and could yield computational techniques never seen before along with a more precise understanding of knowledge representation. A process not too dissimilar to microbiologists piecing together cellular machinery while gaining promising pathways for pharmaceuticals and chemistry. A vision like that, utility aside, is captivating.

Tic Tac Toe Transformer

As a first look into the world of Mechanistic Interpretability, I started a small project with Jack Strand (with some great input from Nick Turner) on a toy model trained on a subset of all possible tic tac toe games. Previous analyses of models trained on board games has given way to interesting mechanistic insights. “Othello-GPT” demonstrated emergent world representations, the world in this case being the game board. Another investigation provided evidence that the Leela chess model performs look ahead in decision making and its attention patterns matched with the available moves that a specific chess piece could make.

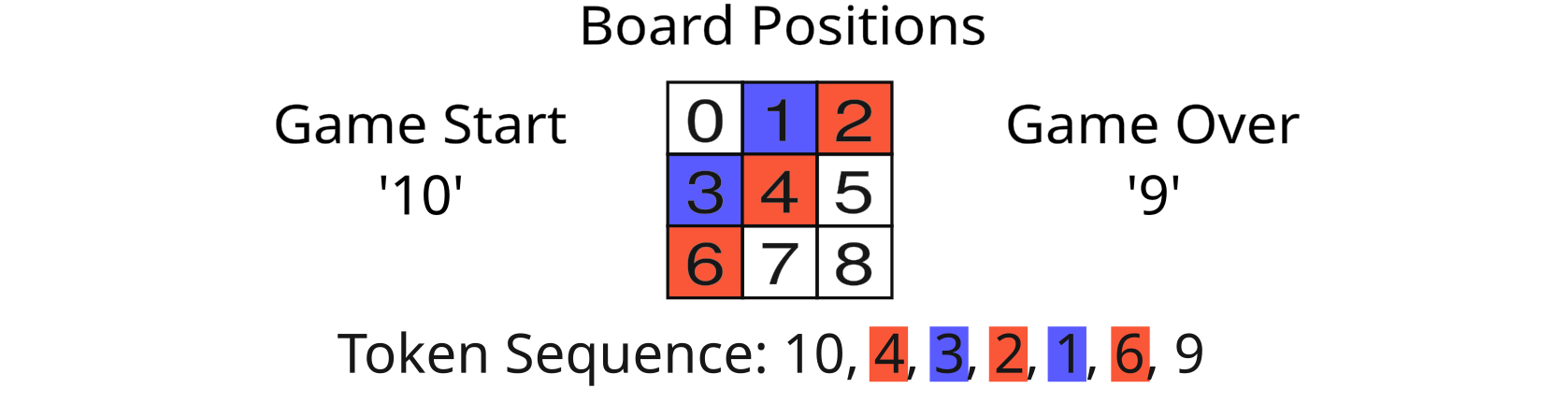
With our tic tac toe model, AlphaToe, the goal was not a model that could play well, but one that would output legal moves and call game over. Tic Tac Toe is of course a simple game, with only 255,168 possible game trajectories. In the ideal trained case, the model should pick a move uniform-randomly over legal moves, and state the probability of game over on a win/loss/draw. A one-layer transformer model was trained to achieve this behavior. The data representation scheme used tokens of 0-8 for the board positions on the 3x3 grid, with token 9 representing game over and token 10 representing game start.

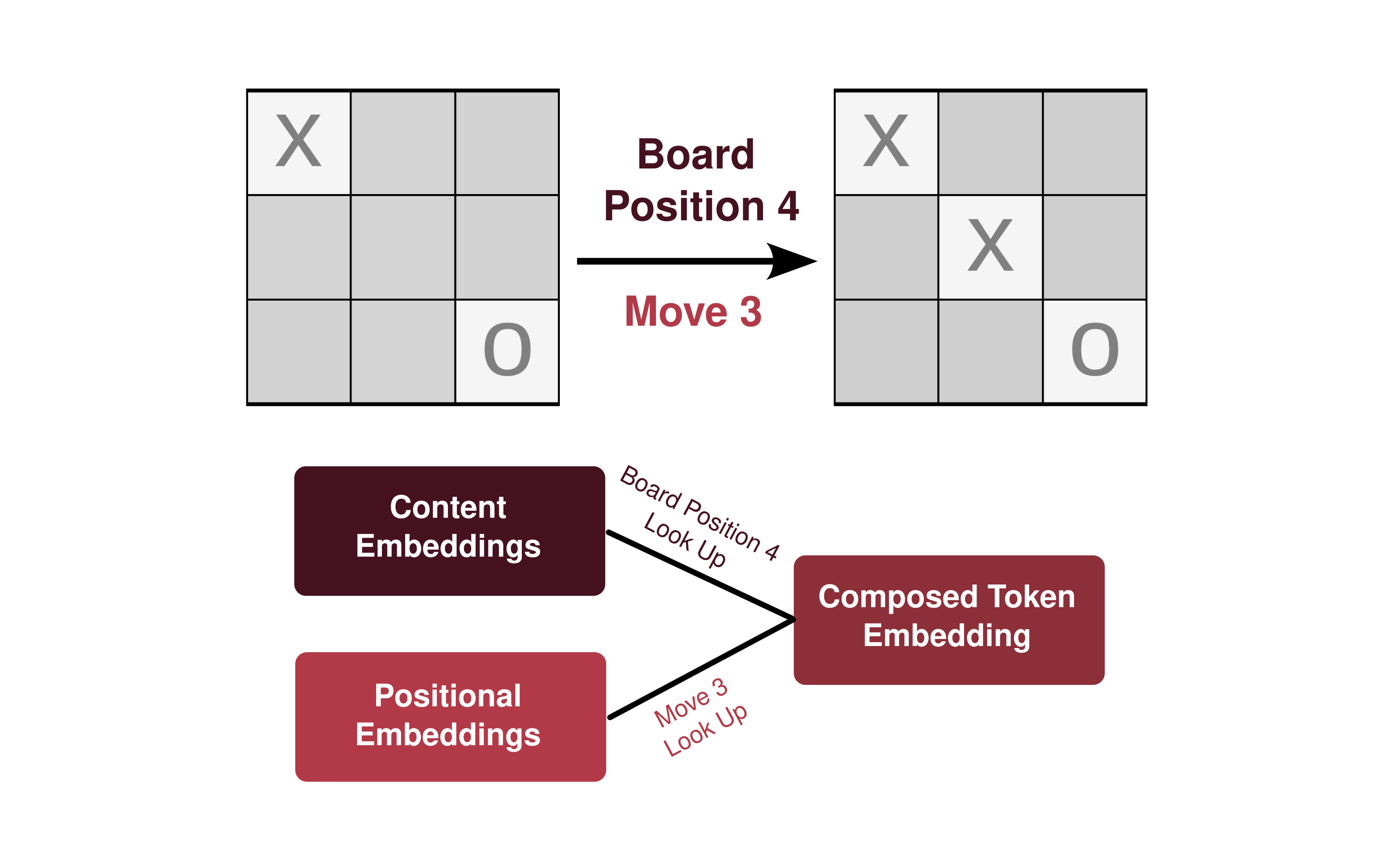
At a basic level our transformer processes each game as a sequence of tokens. The tokens are transformed into a high dimensional embedding representation where each token representation has two key components: a content embedding and a positional embedding. Both embeddings are high dimensional vectors pulled via look up from a set of embedding matrices that are optimized during training. The content embedding represents what is being played, board positions 0-8 or special tokens 9 (game over), 10 (game start). The positional embedding represents when in the sequence of moves the board position appears. For example, playing position 4 (center square) as the 3rd move would sum content embedding for board position 4 and the positional embedding for move 3. I find it helpful to think of these embedding vectors not as abstract points in high-dimensional space, but as objects with many learned properties. A content embedding might encode properties like “part of the middle column”, while positional embeddings might capture “player identity” or “late-game move”. As we’ll see, the model learns to encode specific properties, like player identity, in these embeddings. The transformer’s attention mechanism then computes relationships between these representations, basically asking which properties of previous moves matter for next token prediction.

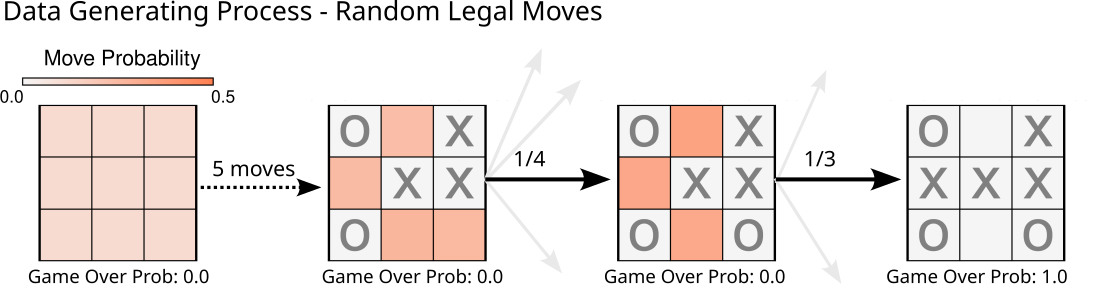
The training labels used to optimize the next token prediction were probabilistic rather than ‘one-hot’. As an example, the model labels/targets for the first move (after start token 10) would be a uniform mass over tokens 0-8 and zero probability for token 9. As the game progresses that uniformity spreads over less and less available tokens until eventually a won/lost/drawn game resulting in a one-hot for token 9 as the target.

Training AlphaToe

The one-layer transformer model was trained with 8 attention heads, each with 32 dimensions, feeding into an MLP of dimension 512 with a 80/20 train/test split. Definitely a bit of overkill but it achieved the sought after evaluation metrics with 0% illegal move behavior, 100% games correctly called as a draw, and 100% games correctly called as won/lost. Mapping success at these evals as a function of the loss curve produces a fairly interesting lesson about model capabilities and dataset coverage. 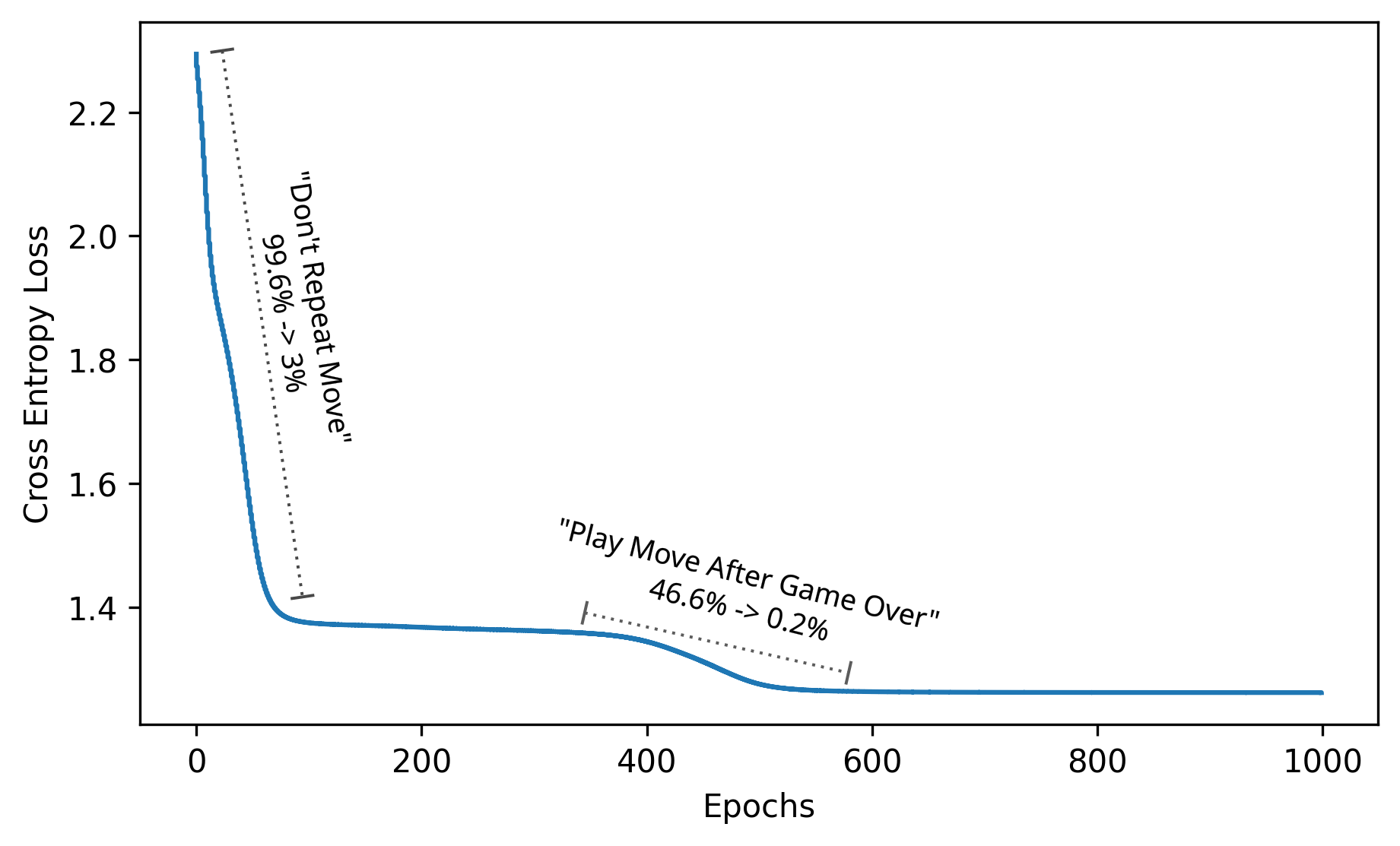The first large decrease in loss corresponds with a major improvement in the ‘Don’t Repeat Move’ error eval. This demonstrates a degree of class imbalance in the objective function. A majority of the training set is predicting random moves played, with zero probability targets for repeated moves. It is also likely a simpler algorithm to implement. If a content embedding is present, don’t assign high logits to that token. Determining win conditions is a more complex algorithm and represented in substantially smaller fraction of the training data. In this case the class imbalance provides a nice visualization over the loss curve of discretely learned behaviors.

Patterns in Logits and Attention Scores

As a first avenue to understand the model, we examined the logit patterns over a given game. To make the visualization simple, we chose a game trajectory where each successive move played is just the next token in the dictionary. The ‘Don’t Repeat Move’ behavior is obvious from this pattern of logits, every previously played move has very low probability assigned by the model. The unplayed board positions have uniformly higher probability as the game proceeds until eventually the game is over and token 9 is assigned nearly all probability (figure below). Simple ablation of the attention heads eliminates the ‘Don’t Repeat Move’ capability effectively demonstrating part of the utility of attention heads in the transformer architecture. The MLP still receives information about the last move played and maintains the behavior bringing the prediction of the most recent move to zero, but does not have access to the previous moves played due to ablation of the attention heads. This at least clues us in that part of the “Don’t Repeat Move” behavior lies with the attention heads.

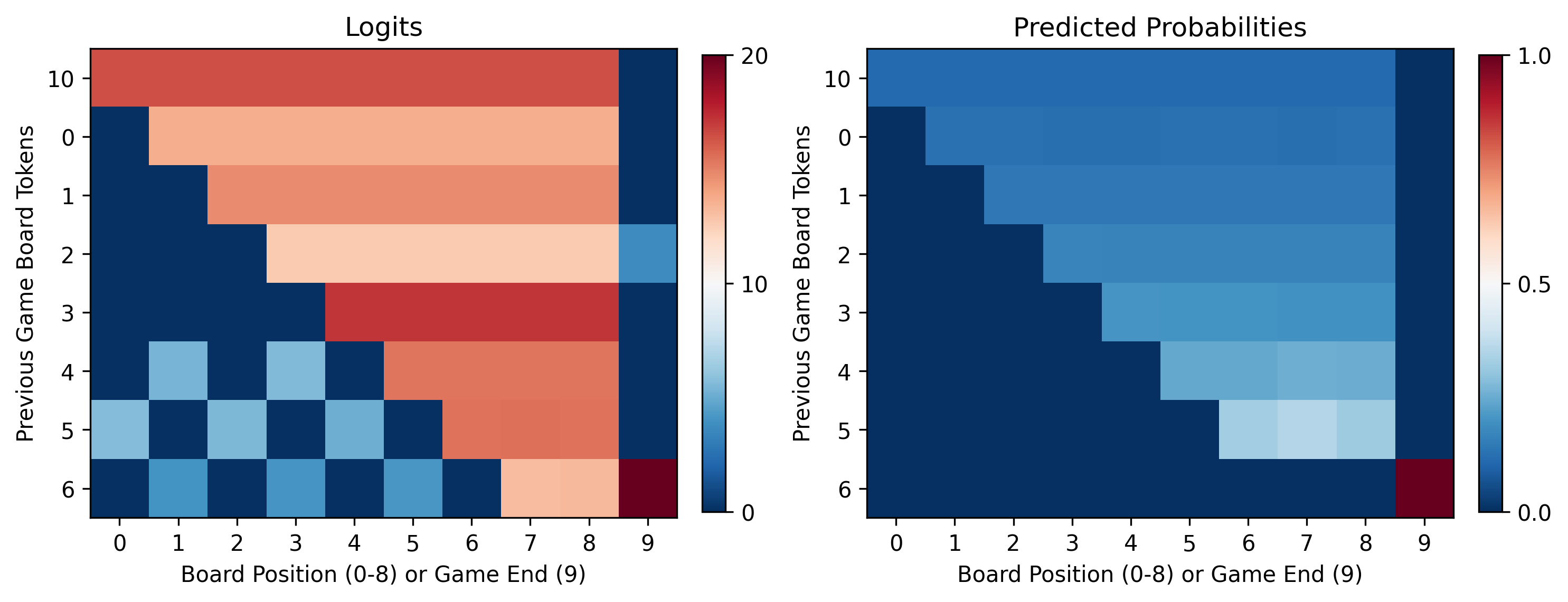
Another interesting element just examining the logits is the alternating, checkerboard pattern seen above. The logits of all previous moves are low enough that they result in near zero probability, but the logits have a pattern dichotomized by player identity. Given the one-layer nature of the model, we assumed this could be an effect downstream of the attention scores.

Visualization of the attention head scores over the course of a game produces the same checkerboard pattern in some attention heads and others a more even distribution of scores. To focus on this specific behavior, we examined Attention Head 1, which strongly displayed the pattern. Plotting the attention scores onto a gameboard we can see that the pattern simply translates to attention score being high for one player and low for the other at least for that attention head (figure below). Specifically, the attention scores are uniform over all previous moves until 5 moves have been played. Then the player aware attention scores emerge. While interesting, this visualization only represents a single game trajectory. 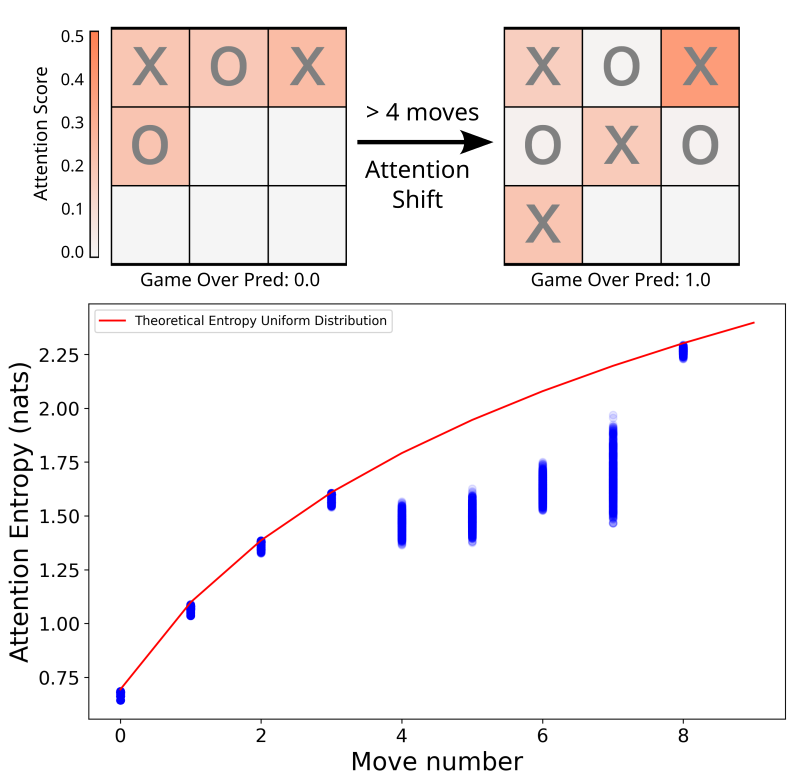To see if the effect is consistent we can measure the entropy¹ of the attention score over other game trajectories, where a uniform distribution would be the maximum expected entropy of the attention scores. 1000 game trajectories were generated to analyze this effect. For moves 0-4 the attention entropy over the 1000 analyzed trajectories matched the maximum entropy associated with uniformity of attention, the maximum possible entropy. For moves 5-7 the entropy drops off the curve for uniformity, until move 8 where it returns to maximum expected entropy. Move 8 is of course where the game is obligate over via win, loss, or draw. The attention score only takes on this bimodal uniform pattern when a game can be won. The model likely learned to only pay attention to the relevant player moves to make a win condition determination.

Positional Embeddings and Interaction with Attention Head 1

The positional embeddings also show the same regular structure. ‘Even’ and ‘odd’ positional tokens have relatively high positive intra-class cosine similarity and lower magnitude inter-class cosine similarity centered around 0.

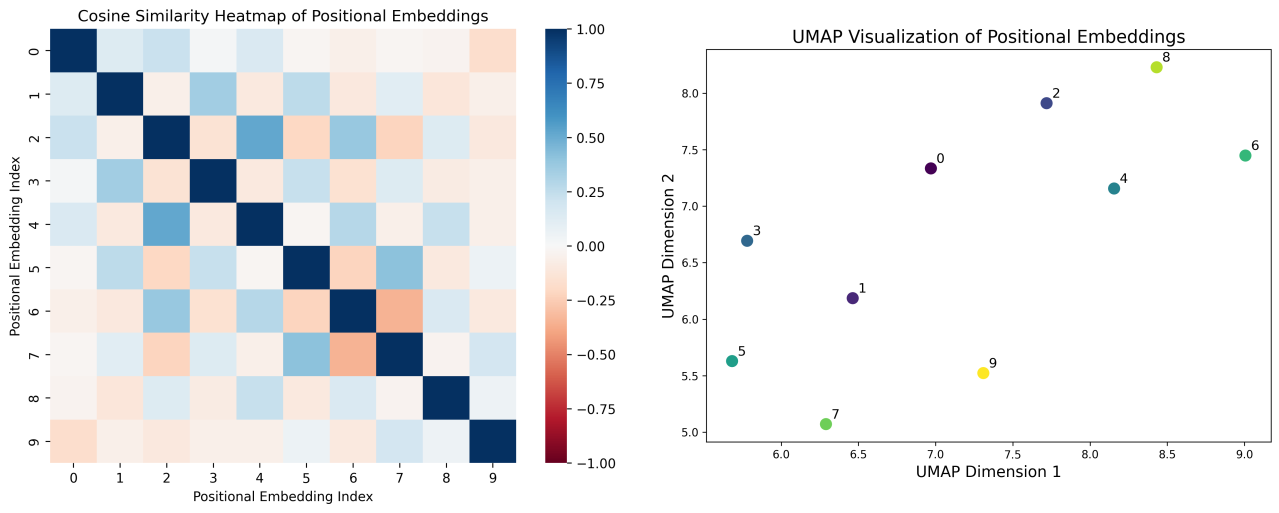
UMAP² clustering tells the same story, with separation between even and odd positional embeddings. The regular structure of the positional embeddings does not fully explain the attention score behavior or why it switches post 4 moves. We dug into the discrete switching of attention score pattern seen in Attention Head 1 through the Query Weight ($W_Q$) and Key Weight ($W_K$) matrices as well as the corresponding Positional Query ($Q_{pos}$) and Positional Key ($K_{pos}$) matrices. The $Q_{pos}$ and $K_{pos}$ were calculated by multiplying the $W_Q$ or $W_K$ with the positional embeddings for a given game state. If you squint very hard at a heatmap of the positional embedding, and $W_K$ and $W_Q$ of Attention Head 1, maybe you can see some interesting structure. However, it becomes more apparent examining $Q_{pos}$ and $K_{pos}$, the products of $W_Q$ and $W_K$ with the positional embeddings.

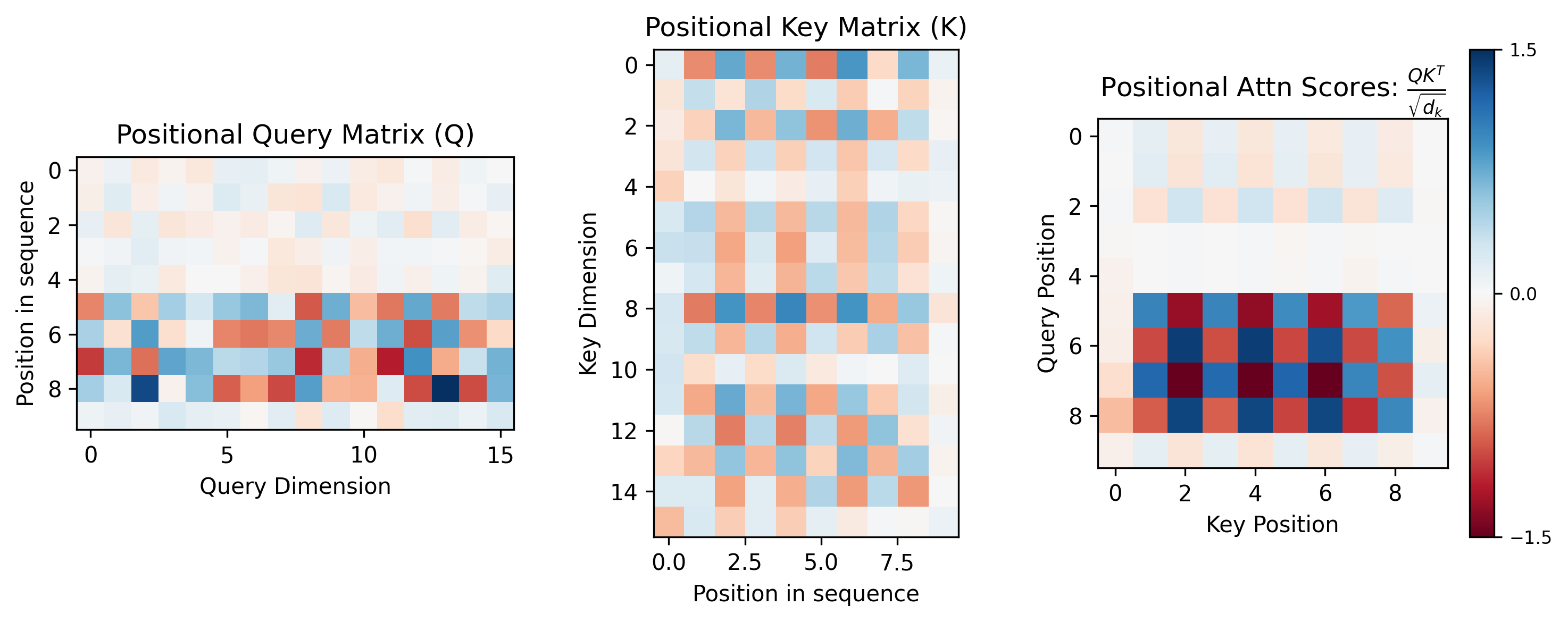
$K_{pos}$ show the alternating structure we are looking for, with high cosine similarity amongst ‘even’ or ‘odd’ positional $K$ vectors. $Q_{pos}$ also shows the alternating structure, however; the structure only exists past positional token 4. Taking the product of $Q_{pos}$ and $K_{pos}$ yields the checkerboard pattern of attention scores. This time only the positional component of those scores. The structure of only having the bimodal attention score past move 4 lies then with the $W_Q$ transformation of the positional embeddings. Taking it a small step further, we can perform SVD ³ on $W_Q$ and see that the first singular value explains a large amount of the transformation. If we perform a reconstruction of $Q$ by taking the product of the positional embeddings with the top singular reconstruction of $W_Q$, the underlying structure becomes even more obvious. 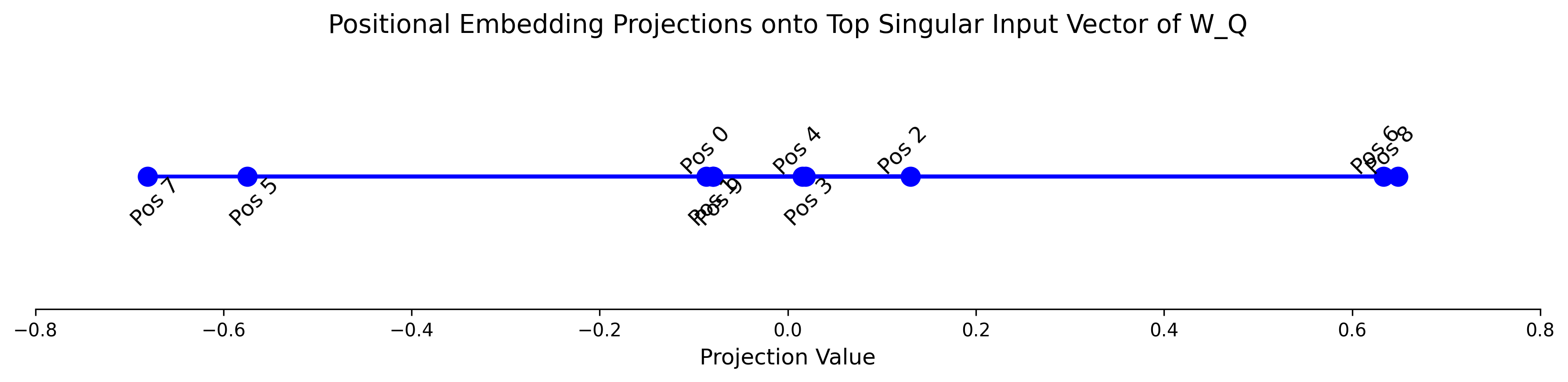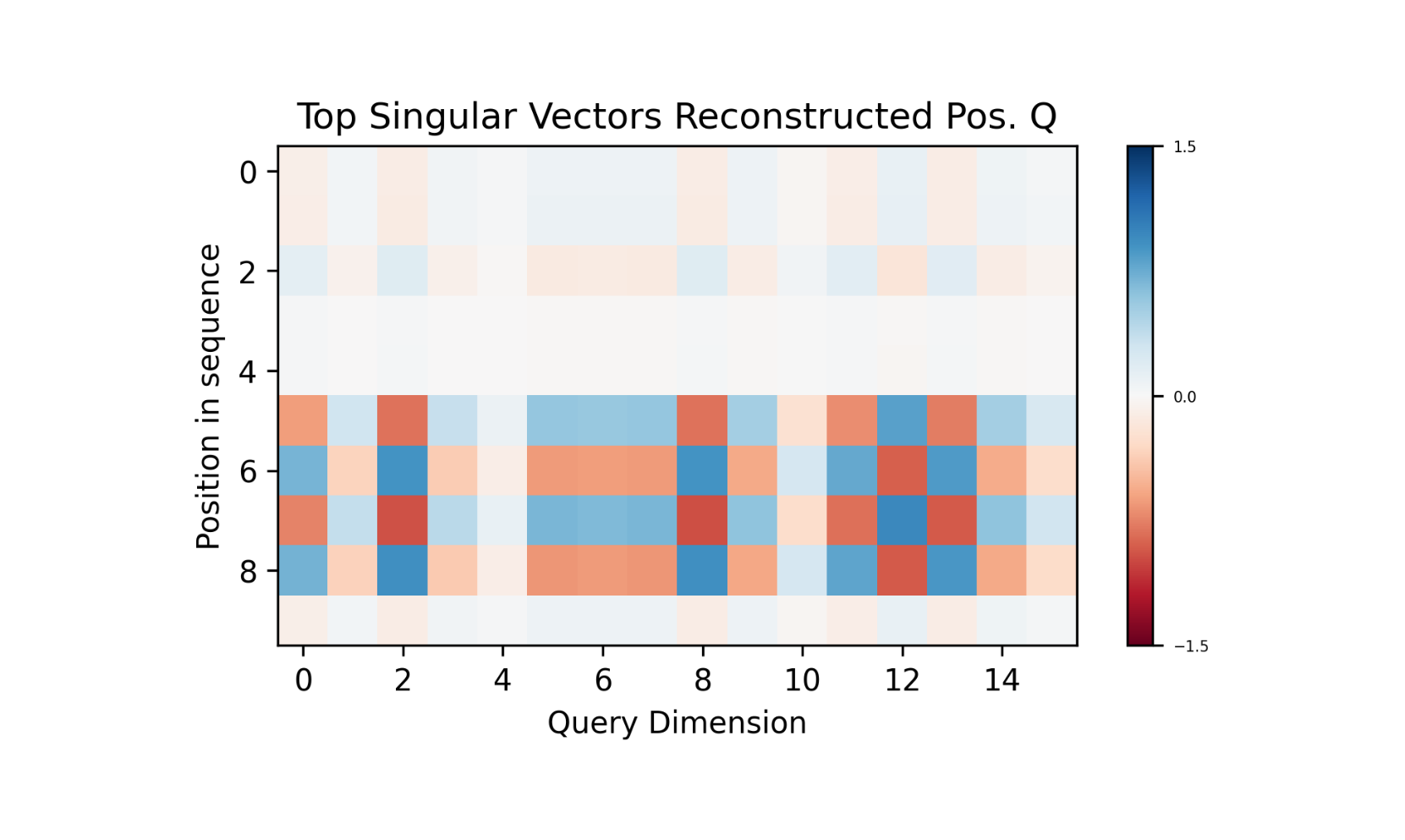To understand which positions are most aligned with the primary query pattern, we computed the projection of the positional embeddings onto the top ‘input’ singular vector $u_1$ from the SVD of $W_Q$. The input singular vectors, $U$, form an orthonormal basis for the input space of $W_Q$, and thus what components of the positional embeddings $W_Q$ acts upon. The scalar projection of $u_1$, the most important vector of $U$, then measures how much each positional embedding contains the feature that $W_Q$ most strongly amplifies when transforming inputs into query space. Upon projection the positional tokens necessary for win conditions (tokens 5-8) cleanly separate into two clusters with high magnitude values. Positions 6 and 8 project to positive values greater than 0.5, while positions 5 and 7 project to negative values less than -0.5. All earlier positions (0-4) and position 9 cluster around zero, indicating they contain little of this player identification direction in embedding space.

This pattern suggests that $u_1$ functions as a learned ‘late-game player identity axis’ in the embedding space. Plotting the positional vectors 5 or 6 along with $u_1$ shows this in 128-dimensional action. Position 5 vector components have flipped magnitude compared to $u_1$, whereas position 6 lines up in direction nicely with $u_1$.

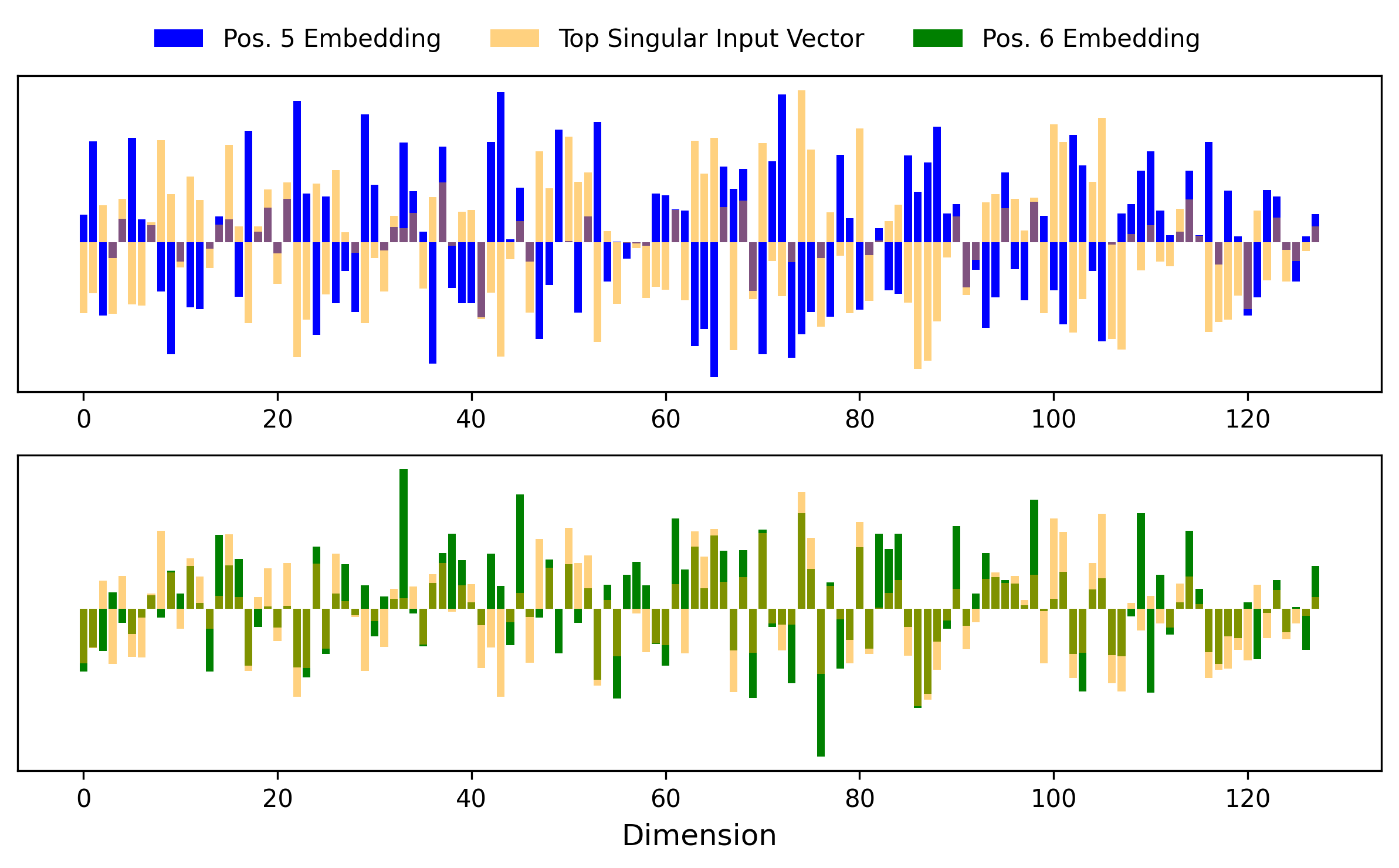
The $W_Q$ transformation is effectively acting as a linear classifier of the positional embeddings. Late-game positions belonging to one player (6,8) align strongly with the axis and are classified in one group. Late game positions belonging to the other player (5,7) align strongly against the axis and classified in the other group. Early-game positions (1-4) remain approximately orthogonal to the axis and belong to neither group. The model has learned that player identity matters for win detection, but only encodes this information when wins become possible. The SVD reveals that this behavioral switch comes both from specific directions chosen in embedding space for the different positional token components along with a classifier tuned to dichotomize those directions while leaving other positions neutral.

As a final examination, we can look at how this player aware attention develops during training. The scalar projection of the positional embeddings onto the first singular input vector provides a good continuous visualization of the separation of the different positions over time.

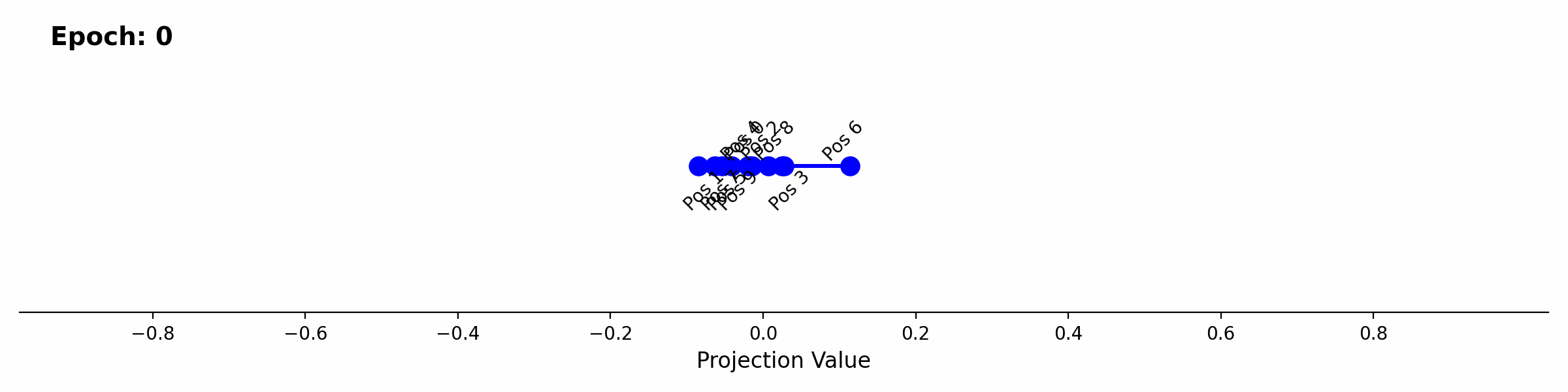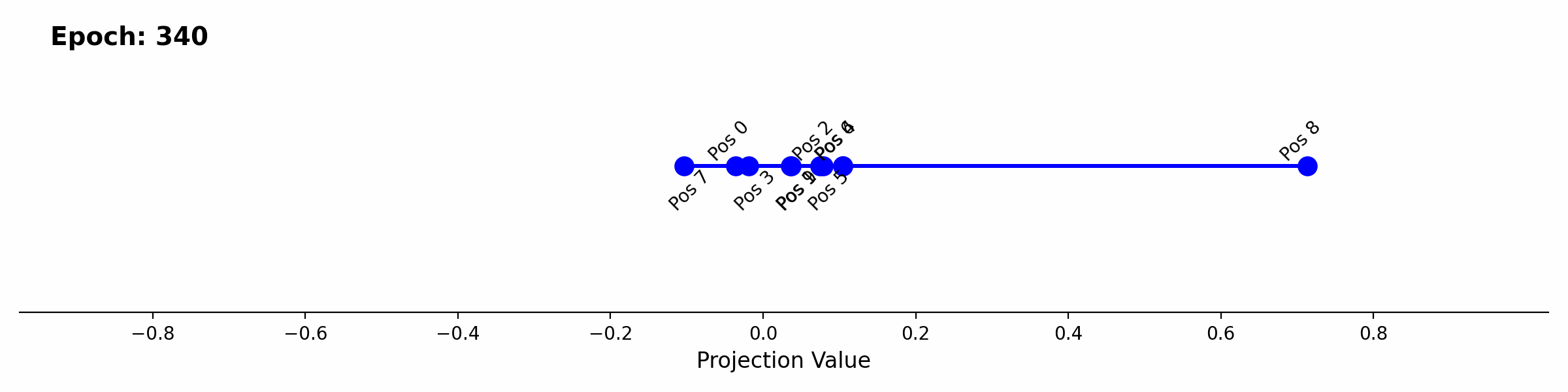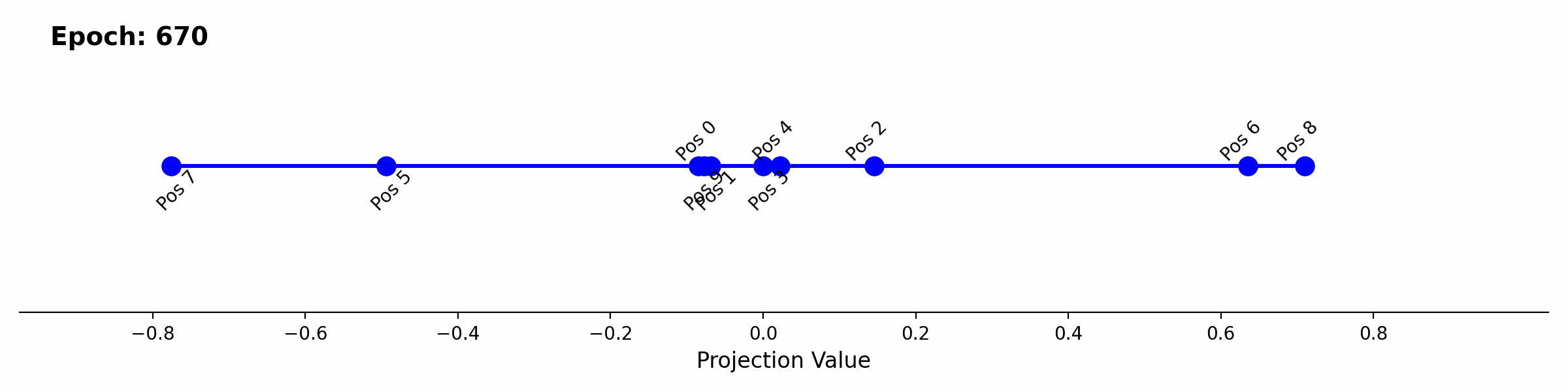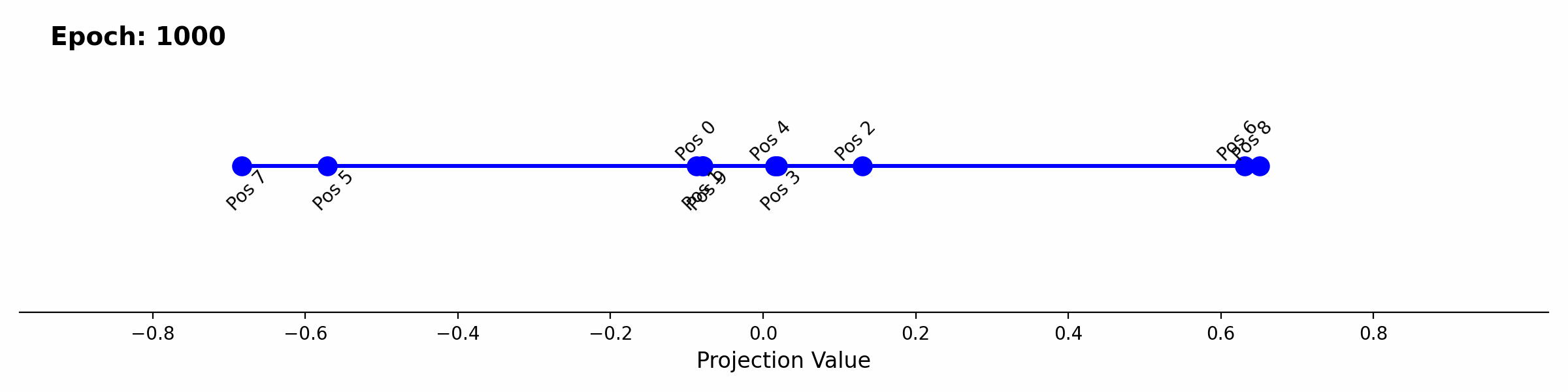
Positional embedding 8 begins separating first, which relates back to class imbalance. 50% of won games end on the 8th move. The imbalance lines up with the loss curve where right before the drop in loss at epoch ~350, the eval around error in predicting a won game sits around ~44% accuracy. After epoch 350 the loss drops rapidly until epoch ~600 with an improvement of the eval to 0.2% error. The drop again lines up with the visualization of positional embedding projection over epochs, where positional embeddings 5, 6, and 7 also separate through epoch 350 to 600.

Final Thoughts

Using SVD of Attention Head 1 we successfully isolated a specific behavior in AlphaToe: player identification for win conditions. This is just one behavior in one attention head in a one layer model. The query matrix of that attention head performs linear classification of positional embeddings such that they have high or low dot product with their corresponding key vectors. We found interpretable structure in a model trained only to output legal moves, rather than play strategically. This suggests that even minimal training objectives can induce meaningful and complex computational structure, with base pieces as simple as linear classification. As mechanistic interpretability techniques mature, we may be able to extract increasingly complex algorithms from larger models.

Footnotes